Quantum Chemistry
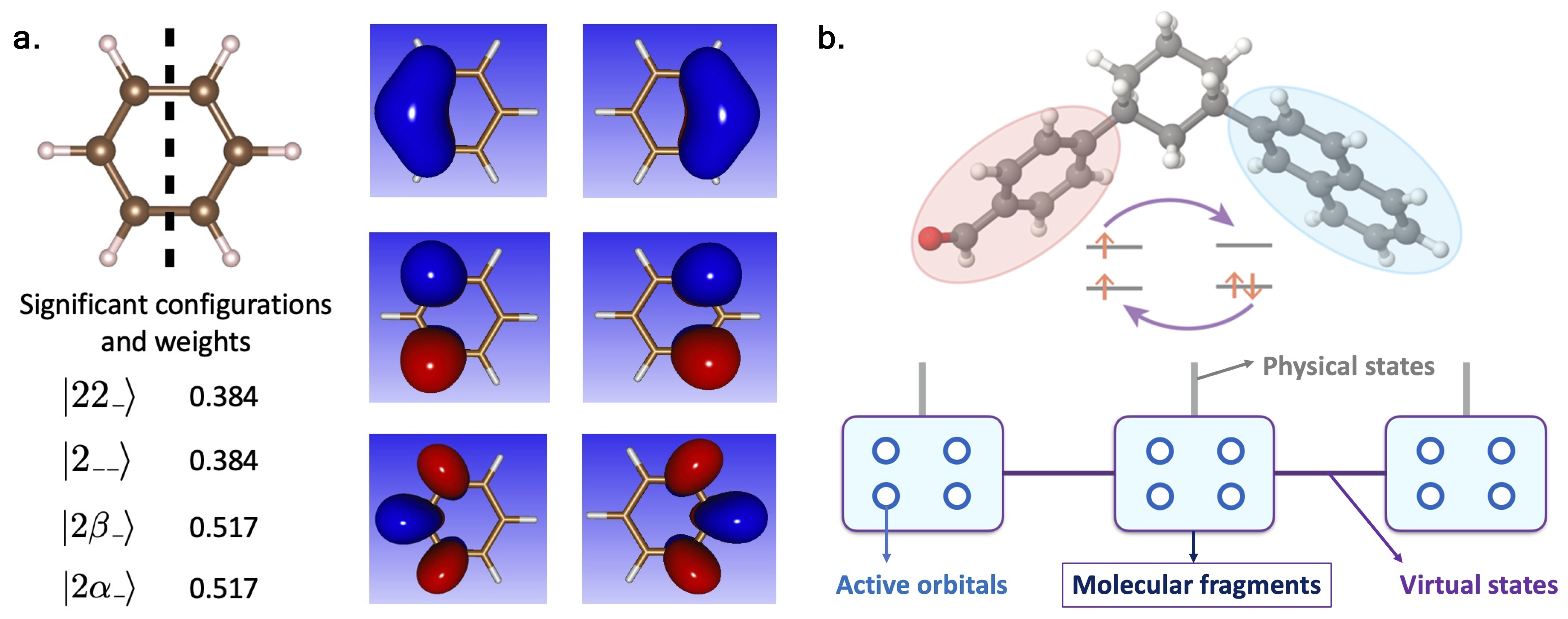
Figure | Schematic of quantum chemistry research. The objective is to model the microscopic electronic wavefunctions of a molecule to accurately calculate its physical properties.
In a nutshell, as a theoretical chemist, I develop numerical models to simulate and understand quantum molecular systems by solving the time-independent Schrödinger equation. My research is mainly focused on developing active space decomposition (ASD) algorithm with second-order orbital optimization, and Douglas-Kroll-Hess (DKH) scalar relativistic approximation methods. I contributed to the open-source quantum chemistry simulation package BAGEL, currently maintained by Dr. Toru Shiozaki and his deep tech startup QSimulate. I find the theoretical framework and computational modelling techniques extremely exciting, which was the main driving force for me to attend Northwestern for graduate studies.
The Wave Function Approach
Our main objective is to solve the time-independent Schrödinger equation, from which we could determine the physical properties of a molecule, in theory. Computationally solving this equation comprises constructing the Hamiltonian operator and formulating the wave functions. Numerically speaking, we employ an eigensolver to approximately diagonalize a huge Hermitian matrix (the Hamiltonian) within a subspace of the entire Hilbert space to obtain the ground state wave function (based on the linear variational method).
However, the time complexity of this step grows exponentially w.r.t. the system size, which makes simulating large molecules (e.g., proteins) at quantum mechanical level extremely challenging. Therefore, theoretical chemists develop novel methods to find a balance between "accuracy" and "efficiency". In other words, we would like to simulate a quantum molecular system as accurately as possible, within an affordable computational budget.
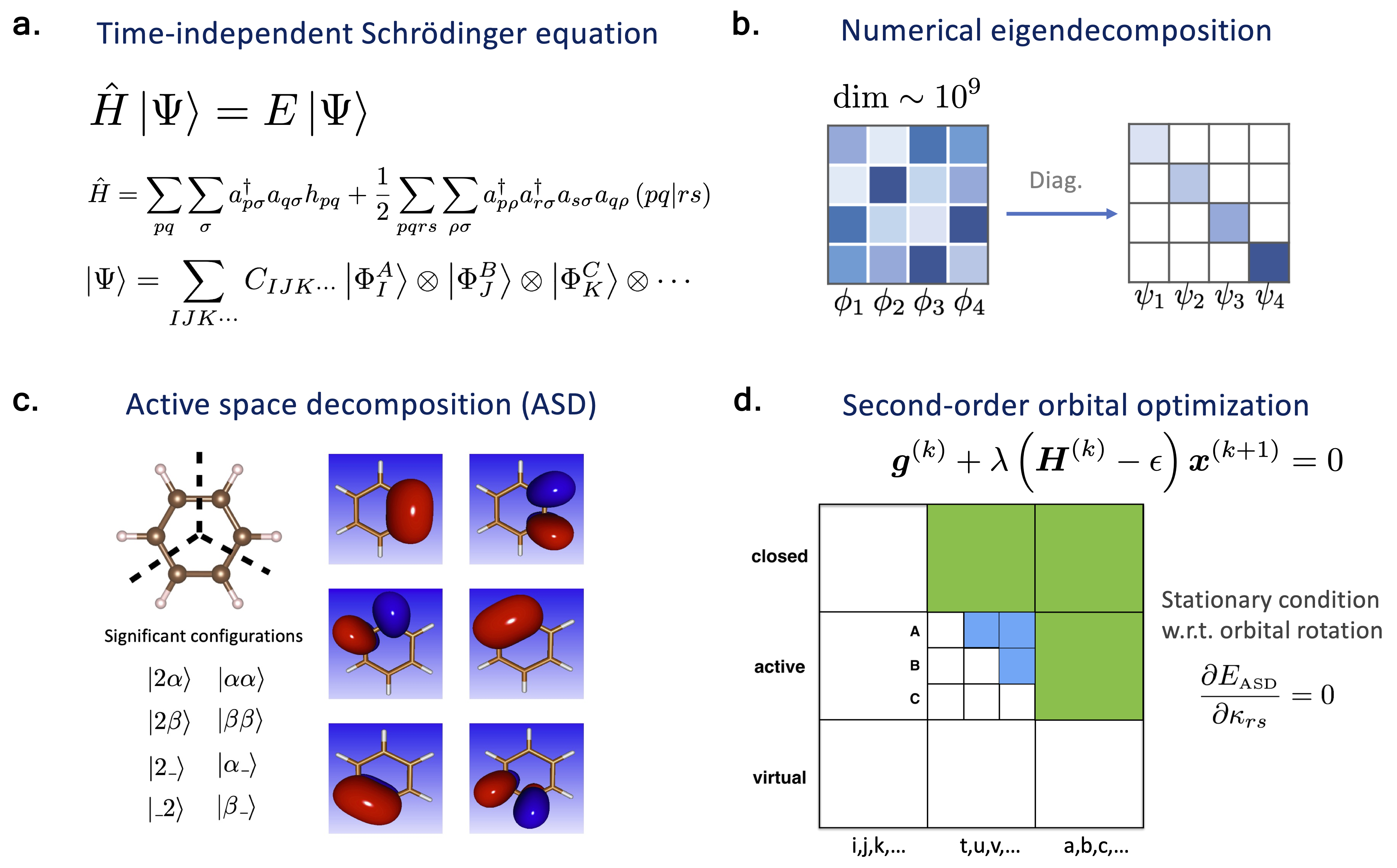
Figure | Overview of the Active Space Decomposition (ASD) algorithm.
Active Space Decomposition
The main idea behind Active Space Decomposition (ASD) is about "divide and conquer". Specifically, we virtually divide the entire molecule into several fragments, i.e., functional groups. Then, within each molecular fragment, we optimize for the most significant electronic configurations to properly represent the state of the fragment. The way we determine the importance of configurations is similar in nature to that in density matrix renormalization group (DMRG) algorithm. For small molecules, we could take all electronic configurations into consideration, and reconstruct the exact total wave function without loss of information. For larger systems, we discard the less significant configurations of each fragment, and combine the most informative states from all fragments to reconstruct the molecular electronic wave function. This way, we can control how much information we want to keep, hence achieving a balance between "accuracy" and "efficiency".
To further optimize for the ground state electronic structures, I also employed second-order orbital optimization on top of the ASD algorithm. In short, this method iteratively solves the eigendecomposition problem within the current subspace and optimizes for a better subspace in which the ground truth lies.
Relativistic Quantum Chemistry
I am also interested in incorporating relativistic effects for quantum molecular systems. Relativistic effects are particularly important for molecules containing transition-metal ions, e.g., Cu, Fe, which are essential elements in human body. For instance, hemoglobin is a protein in red blood cells which contains Fe ions and binds to oxygen, allowing the blood to transport oxygen from the lungs to the rest of our body.
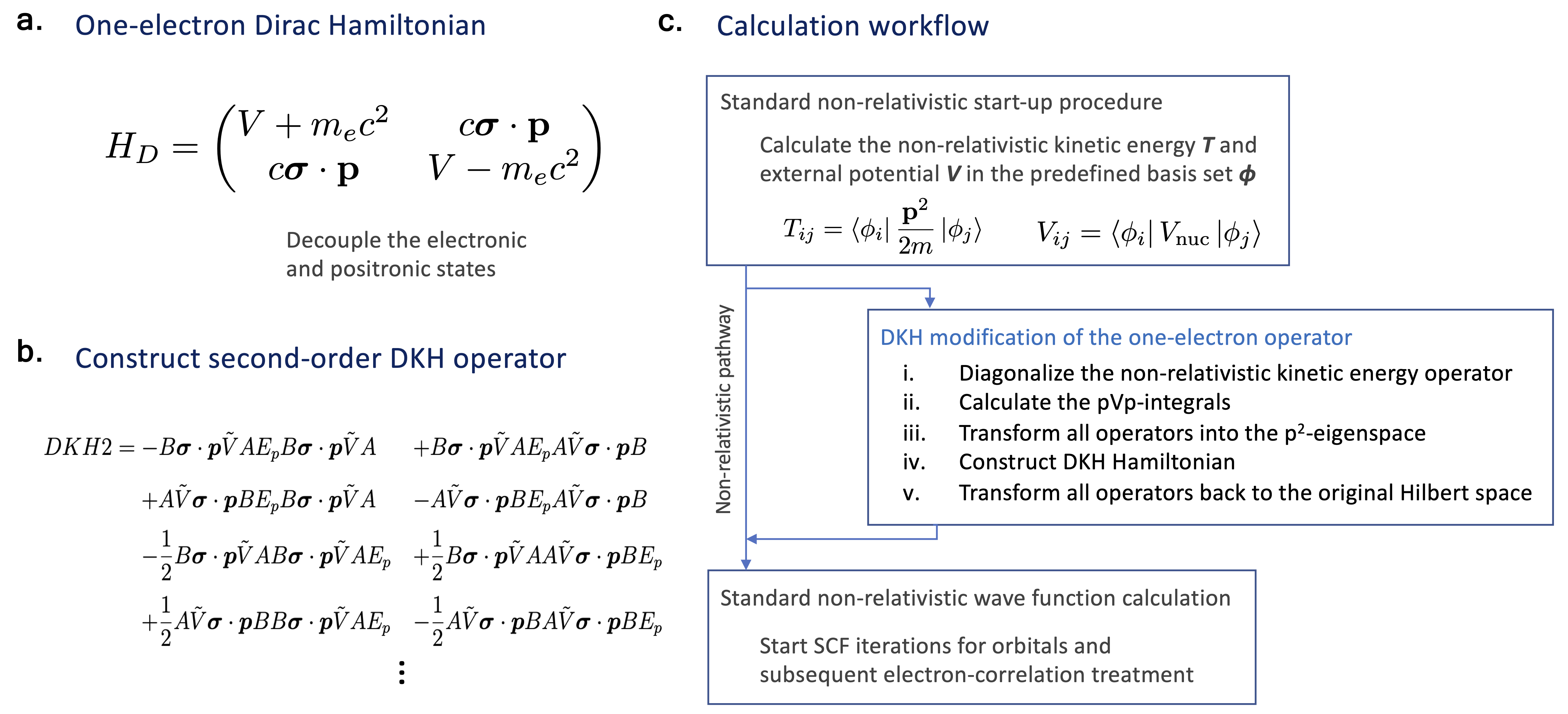
Figure | Workflow of the SCF solver with DKH scalar relativistic approximation.
I developed scalar relativistic models based on the Douglas-Kroll-Hess (DKH) algorithm. Compared with non-relativistic models, our formulation is slightly more complicated but achieves better numerical accuracy at affordable computational cost. The theoretical details is out of the scope of this post, but I am happy to discuss if you are interested. I personally find making derivations and implementing these models extremely exciting, especially when the first time my model works.
