Better Materials = Better Life
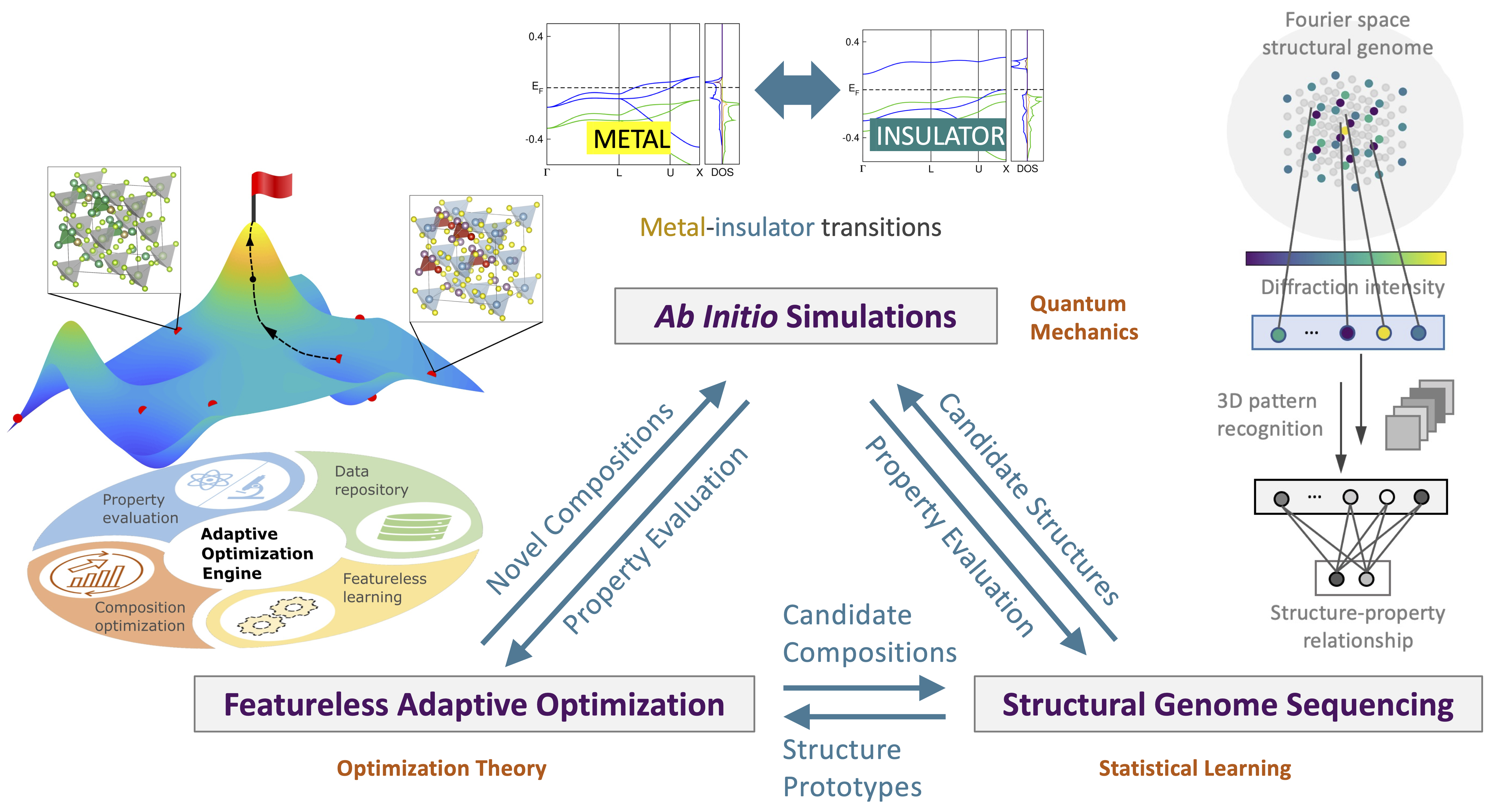
Figure | Data-driven electronic materials design and discovery roadmap. By leveraging first principles simulations, statistical learning models, and adaptive optimization algorithms, we achieve a more cost-effective design framework for novel electronic materials.
During my Ph.D. studies, I developed a data-driven framework for electronic materials design by weaving together several research subdomains: first principles density functional theory (DFT) simulations, materials informatics, and optimization theory. The intricacies of electronic materials, deeply rooted in condensed matter physics and quantum chemistry, often revolve around inorganic crystals with periodic boundary conditions. The complexity of materials systems helps me realize the immense value of interdisciplinary research, whose strength lies in uniting scientists and engineers from diverse backgrounds, fostering collaboration to address prevailing challenges.
Adaptive Optimization for Materials Design
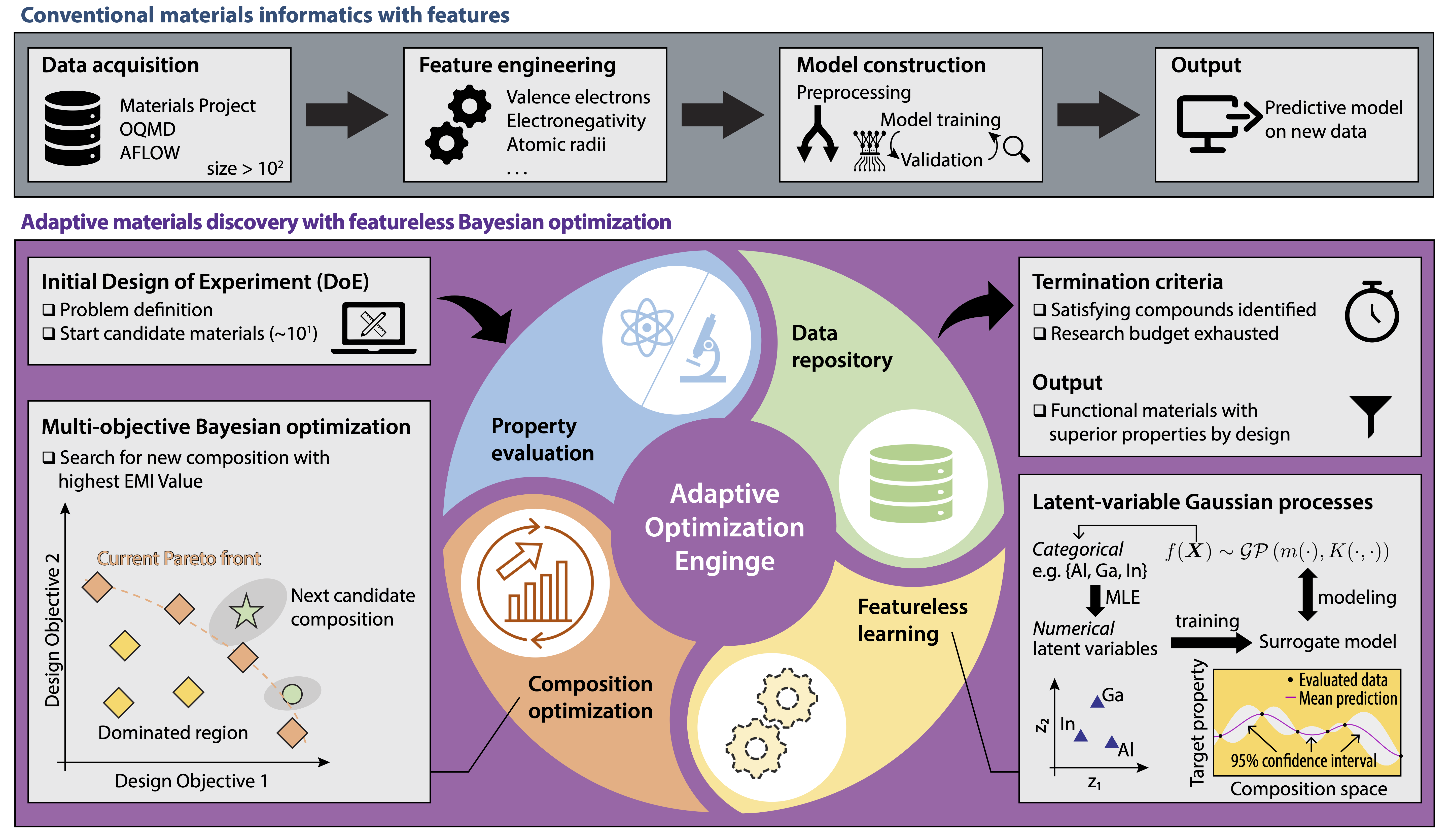
Figure | Upper panel: The workflow of a conventional feature-based machine learning model. Lower panel: The adaptive materials discovery scheme.
This general workflow helps materails scientists effectively identify candidate compounds exhibiting superior functionality by design. The optimization scheme starts from an initial set of design of experiments, where system variables, design objectives, and design space are first defined for the problem. Property evaluation: The target material properties (i.e., design objectives) are evaluated either by experimental measurement or theoretical simulations. Candidate composition and its evaluated properties are then added to a Data repository, which initially may either be empty or only contain entries for existing materials within the design space. Its size grows as more candidate materials are evaluated during the adaptive optimization process.
Animation | The adaptive optimization trajectory, where grey diamonds are the initial DOE set, blue circles are newly explored compositions, and orange stars form the design Pareto front.
Featureless learning involves directly learning from the chemical composition of materials comprising the data repository by mapping each compositional variable into a two-dimensional latent space using maximum likelihood estimation, which enables the construction of a latent variable Gaussian process (LVGP) surrogate model. Composition optimization: Multi-objective Bayesian optimization is then performed with the LVGP models to obtain the next candidate material composition with the highest expected maximin improvement. The iterative optimization continues until all compounds satisfying the objectives are discovered, forming the Pareto front, or research resources are exhausted. See details here.
Materials Informatics
When we talk about materials "structure-property relationship", a more precise description ought to be "structure-composition-property relationship", since the 3D arrangement of atoms as well as their atomic species co-determine materials properties. One would naturally ask: how does structure alone impact materials properties? The answer to this question helps us optimize materials functionality through perturbing their atomic structures (e.g., applying pressure).
Machine learning offers a unique perspective to this question. By marginalizing chemical composition information in crystalline materials and perform statistical analysis via a trained deep neural network, we study the response of various materials properties to crystal structures without chemical compositions. Our secret sauce is that X-ray diffraction patterns preserve 3D structure information, while discarding partial compositional information (due to the infamous phase problem). We train a deep neural network to learn from the diffraction patterns for multiple materials property classificaitons, and analyze how different structures influence these properties. We find that crystal symmetry is more important than the diffraction intensities contained within for the model to make a successful classification.
Our work also showcases the potential of using machine learning models to help understand materials physics, rather than performing predictive or generative tasks as in most materials informatics research. We also argue that learning the crystal structure genome in a chemistry-agnostic manner demonstrates that some crystal structures inherently host high propensities for optimal materials properties, which enables the decoupling of structure and composition for future codesign of multifunctionality. See details here.
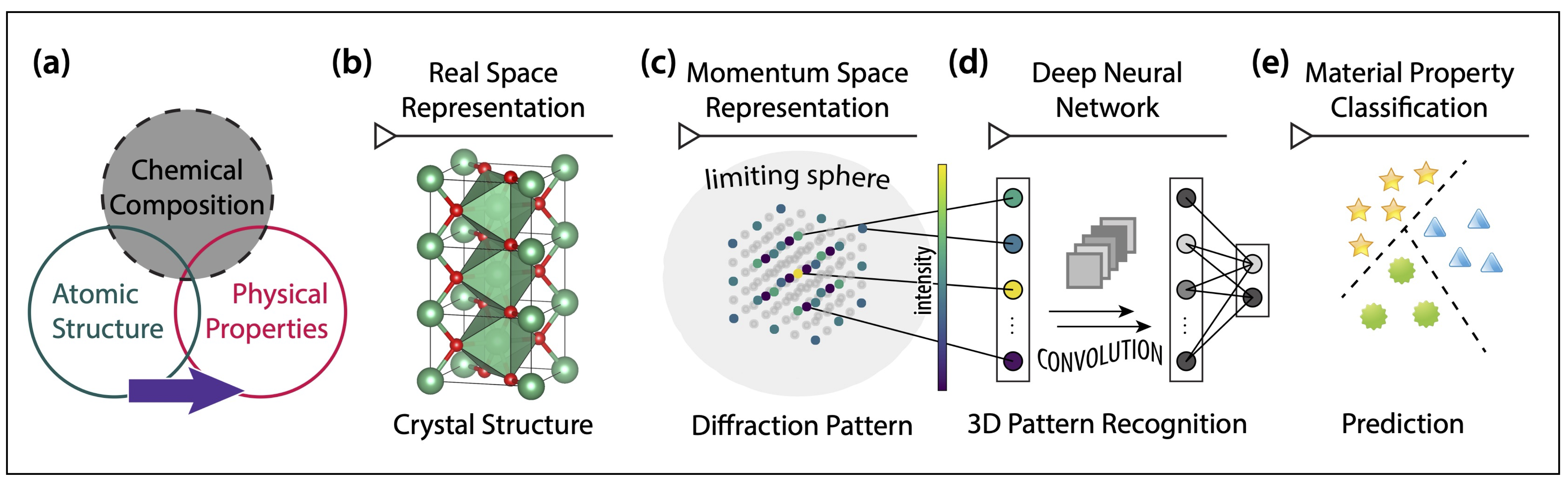
Figure | Learning Fourier space crystal structure genome for property classificaitons.
One of my most influential work explores the potential of using symbolic learning to reveal some governing physical laws from a large amount of data. Symbolic regression has recently garnered much attention from the scientific research community owing to its form-free learning mechanism, which makes it an ideal tool for materials scientists to analyze their experimental data. See here for more details.
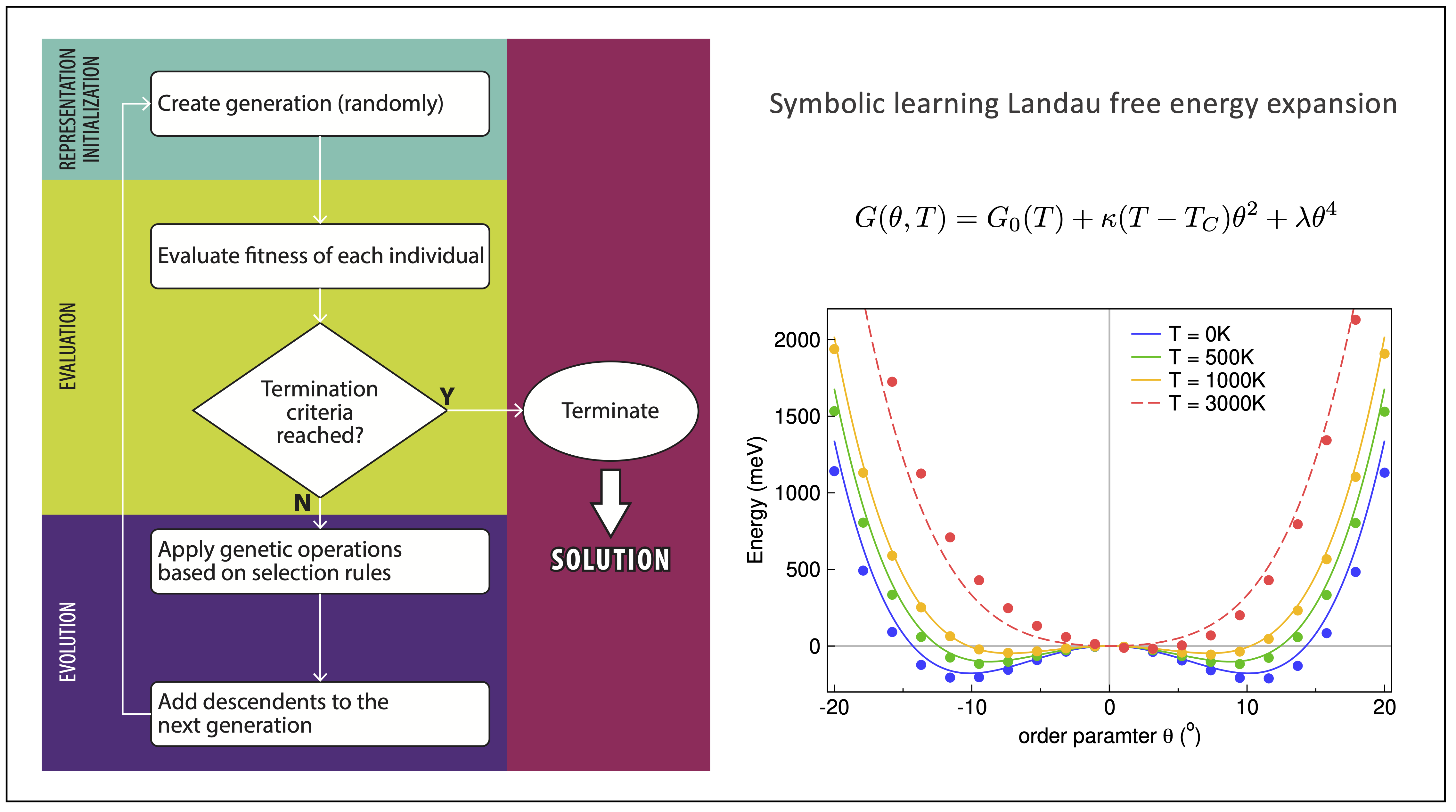
Figure | Symbolic regression and its applications in materials science.
Ab Initio Density Functional Theory Simulations
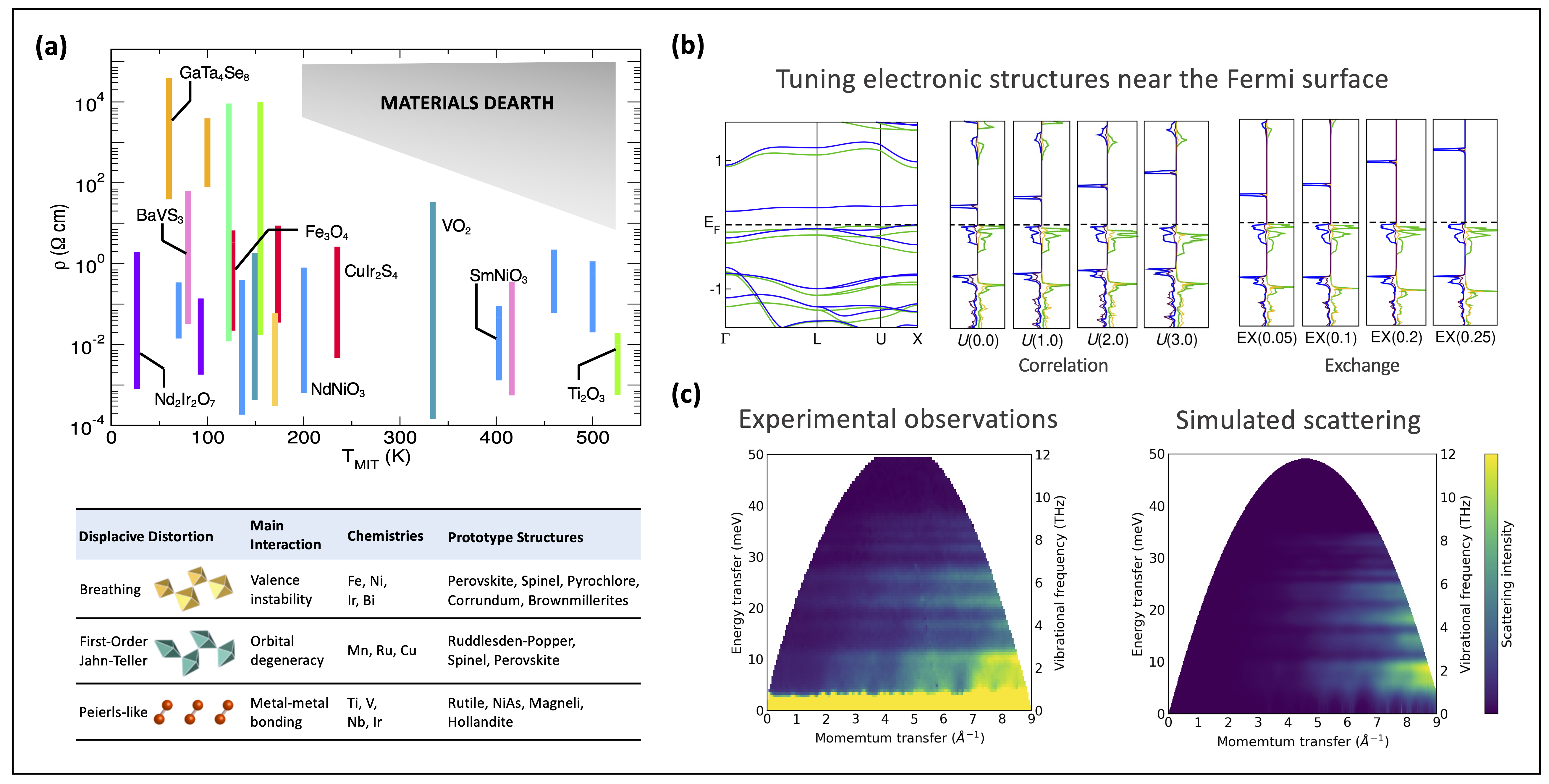
Figure | (a) The range in resistivity accessible across the phase transition of a variety of materials exhibiting metal-insulator transitions. (b) We study the structure-property relationship of crystals using first principles simulations and (c) compare with experimental results.
I also have experience employing density functional theory (DFT) simulations on electronic materials systems. Unlike the theoretical nature of my quantum chemistry research projects, this work is more application-driven and involves more simulation-running tasks, whose goal is to identify ideal compounds for novel electronic materials platforms. Indeed, inorganic crystals are quite different from molecular systems (more is different). There is so much that I would like to talk about regarding this topic (e.g., its relationship with the "scaling law" in AI research). Don't hesitate to reach out for some further discussions!
